此模型已經與中國,瑞典和美國的數據進行了驗證,採用報告的隨時間死亡的數據進行參數估計。
模擬預測結果吻合實際的傳染曲線。 此案例調查不同的隔離措施對流行病傳染模式的影響。
翻譯COMSOL 部落格文章,原始出處:
https://www.comsol.com/blogs/modeling-the-spread-of-covid-19-with-comsol-multiphysics/
病毒粒子在活細胞外生存的能力非常有限,因此傳播病毒的主要機制是透過生物體之間的接觸。在SARS-CoV-2,導致新型冠狀病毒疾病COVID-19的病毒,它必須直接或間接地從人類傳染給人類。COVID-19已被世界衛生組織(世衛組織)列為大流行。
但是,能否瞭解這一流行病的進展?有多少人會感染?有多少人會死?讓我們看看這樣的模型會是什麼樣子。
COVID-19 的數學模型
對人際傳播合理預測最簡單的模型之一是所謂的SEIR模型,該模型在20世紀20年代左右以第一種形式發佈(參考文獻1,"SIR模型和公共衛生基礎")。它把流行病期間的人口分成四個不同的隔間,每個隔間中的人數有不同的變數:
S = 易感
E = 暴露
I = 傳染性
R = 復原和免疫

S、E、I
和 R 變數的單位以個人數量表示。為了使易感艙中的個體暴露,必須與感染者有某種接觸。這種接觸的概率與受感染者比例乘以人口中易感人群數的比率有關。因此,經過一些重新排列後,暴露率為:
(1) 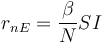
其中 α 是傳輸速率。
* (單位:1/天)
與感染者平均感染的個體數量、R0和一個人具有傳染性的平均天數(在隔離或自我隔離之前)有關,n id:
(2) 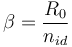
R0 被稱為基本生殖編號(無維度),並描述了在感染者康復前與易感者(當人群中根本沒有免疫力)接觸時疾病的傳播情況。任何緩解或遏制策略都將旨在透過降低傳播速率*或感染個體被隔離之前的時間來減少繁殖數量。
對於較短的(非季節性)流行病類比,我們可以假設一個固定的人口,其中自然死亡和出生是平衡的。然後,易感個體的數量隨著新暴露病例的增加而減少,其中N 表示人口的大小:
(3) 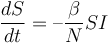
相應地,上述方程右側的術語是公開數的方程中的源術語E。然而,這個方程也有一個負術語,對於那些暴露離開E艙,並成為傳染性。
(4) 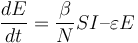
此處, * 表示一旦暴露,每天單位(1/天)的傳染性進展率。速率與潛伏期的長度成反比。
傳染性,I,每天隨+E增加E,但隨著個體被隔離、恢復或死亡的速度而減少。讓速率係數 = 表示人們隔離或恢復的速率。速率與感染的天數成反比,根據:
(5) 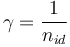
還有一個術語,用於感染疾病+I的死亡率,以及受感染變數I的方程I,因此成為:
(6) 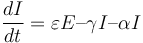
R 變數表示R不再易受攻擊的個體的方程是:
(7) 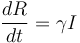
死亡人數的方程DD是:
(8) 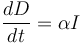
拼平曲線
我們可以從查看更簡單的模型開始,其中未考慮公開的變數;即,易感個體與受感染者相遇並受感染。在我們的模型中,這將對應於一個非常大的值 * 。然後,我們可以將其與邁克爾·赫勒的博客文章進行比較,因為他已經解決了相同的方程數(參考文獻2,"將COVID-19曲線平展")。輸入資料如下:
N = 100 萬個人
R0 = 2.25,基本繁殖號
nid = 5 天
最後,我們需要初始條件:
S0 = N = I0 易感個體
I0 = 10 感染者
在第一種情況下,Höhle 進行類比,允許流行病在不受人口社會疏遠的限制的情況下進行。在第二個案例中,Höhle假定擁有100萬人口的城市當局採取行動減少繁殖數量,例如不允許聚集更大的人群(體育賽事、音樂會等)。第一步是透過在社會交往中引入限制,在流行28天后將基本繁殖數量減少到1.35。當行動放鬆時,這種減少將持續五周,然後允許繁殖係數再次增加到1.8。下圖顯示了兩種情況:案例 1(無操作)和案例2(R0的縮減)。我們可以看到與Höhle的結果非常一致。

案例2(Höhle)得出的有趣結論是,為減少新病例的再發而採取的行動不僅減少了任何給定時間的新病例數量,而且還減少了在流行病消失之前感染的人數。結果如下圖所示。在流行病消失之前感染的人口比例為85%,而在病例2中,只有68%。因此,行動不僅暫時減輕了醫療系統的負擔,而且減少了整個流行病中患者總數。

流行病發展過程中人口分佈的核算
對於湖北、瑞典和美國,我們可以使用稍微先進的模型,即所謂的Erlang_SEIR模型(參考3,",
“二郎流行病模型的離散隨機模擬")。透過將 E和I隔間劃分為子隔間,每個隔間中的個體的居住時間將遵循 Erlang 分佈,其指定的平均居住時間與子隔間數 k E 和 kI成正 比,與子隔間之間的傳輸速率成反比。此模型可以解釋不同隔間之間的流動分佈,例如,由於暴露的病例在該國不同地區的不同時間進入。增加子隔間的數量將分佈集中在平均值上,有效地引入了從E到 I 以及從 I 到
R 和 D的進度的延遲。
The Erlang–SEIR
model with subcompartments for E and I.
中國封城模型
我們可以使用此模型,對疫情開始所在的湖北的數據進行參數估計。我們知道,受感染的人數不是可靠的數據,因為大多數人沒有經過測試或給予COVID-19診斷(參考,
“4,"2019年冠狀病毒疾病嚴重程度的估計:基於模型的分析")。最可靠的數據可能是死亡人數。
假設死亡率為0.66%(參考文獻4),平均在隔離前傳染3天,平均從癥狀開始到死亡18天,我們可以適應疫情的開始率、傳播率和在二郎分佈到湖北報告數據中暴露狀態的平均時間。
1月22日,當局實施封鎖,到當月底,測量顯示基本繁殖數量明顯下降(參考文獻,
“5,"COVID-19傳播和控制的早期動態:數學建模研究")。
如果我們實施這種削減,並且如果我們與1月23日開始的減少效果相適應,我們會得到以下結果。
The modeled data
for the number of deaths compared to the data reported in Hubei. We can see
that the model is in good agreement with data, with a small shift of a half a
day to a day. This shift could be explained by a delay in reporting as the
number of deaths increase. The smaller graph shows the same data in a
logarithmic scale for the y-axis.
我們可以在上面的圖中看到,到2月2日,累計死亡人數呈指數級增長,在對數圖中呈線性增長,直到大約400例死亡。2月3日之後,死亡人數的增長速度下降,使增長不再呈指數級增長。這是由於社會交往的限制。免疫病例的影響,也將限制COVID-19的繁殖數量,目前尚未看到。
下圖顯示了該流行病在暴露病例數、感染病例、康復病例和死亡人數方面的發展情況。我們在 1 月
23 日操作實施時插入了額外的網格線;1月26日中午,發生最大感染人數;和 2 月 3 日,當處於臨界狀態的最大個人數量發生時。請注意,已恢復的病例數是指不再具有傳染性且正在恢復的病例。在醫院裡,這些病人直到一兩周後才被釋放。

湖北疫情的發展。隨著時間的推移,預計受感染的人數將接近500,000 人。
如果我們進一步觀察已恢復的病例,我們可以看到,該模型預測了近50萬人在疫情90天后已經或已經感染了病毒。這比確診病例多7倍以上。這也符合其他調查,因為武漢市只有約15%的感染者登記(參考文6,"大量無證感染有助於新型冠狀病毒(SARS-CoV2)的快速傳播",而且許多感染者要麼不報告癥狀,要麼沒有接受COVID-19檢測。
從參數估算到湖北數據獲得的基本繁殖數為3.03,高於世衛組織報告,但遠低於其他研究報告的範圍(參考文獻,
“7,"COVID-19的繁殖數高於SARS冠狀病毒")。社會分離將繁殖數量減少到約0.56,我們透過適應死亡曲線獲得。這一數字低於其他地方報告的數位,但與當地流行病迅速死亡的情況一致。
瑞典人彼此保持距離
瑞典選擇了不同於湖北和大多數其他國家的戰略:社會交往有限制,但遠非像湖北那樣完全封鎖。因此,建模與湖北略有不同,而且自第一例感染和暴露病例從義大利和奧地利輸入以來也是如此。我們使用與寒假有關的傳入病例的分發,這些病例分佈在全國各地的三周內。然而,在2月17日至3月1日兩周內,大多數旅行者可能接觸到義大利疫情呈指數級增長,當時斯德哥爾摩地區的居民已經返回家園。
以下是類比死亡與報告死亡數相比。4 月
2 日病例的生長呈指數級(對數圖中的線性)。

The number of deaths
due to COVID-19 in Sweden. The last reported value on day 33 corresponds to
April 2. The smaller graph shows the same data in a logarithmic scale for the
y-axis.
從參數估計到瑞典數據獲得的基本繁殖數為2.95,與湖北(3.03)獲得的基本繁殖數一致。進口案件總數估計約為500宗。
自3月16日左右以來,社會交往中的限制一直有效,但大多以建議的形式出現,可能沒有立即生效,因此,在死亡人數上尚未看到這種影響。我們在此模型中假定這些限制在 3 月
20 日完全生效。
讓我們假設兩種情況:第一種方案,即社會交互的減少係數為 0.35;第二種情況,此還原為 0.30。第一種情況將繁殖次數減少到1.03;即,每個感染者平均感染1.03個人。第二種情況將生殖因數降低至0.88,低於1,這意味著在10名感染者中,只有9個(幾乎)可以在恢復前"替換"自己(平均)。
這兩種情況下的削減都不如湖北的限制那麼大,這是一個合理的假設,因為瑞典沒有實施完全的封鎖。
在第一種情況下,約有210萬人受到感染,約佔人口的20%(見下圖)。截至4月2日,感染或感染的人數為28萬人,幾乎是確診病例的60倍。第二次病例導致截至4月2日約有26萬人感染,但疫情進展大大減緩和受阻,導致在疫情消失之前,有時感染病毒的人略低於100萬人。

Total number of
infected, accumulated, in the two case scenarios in Sweden. This is the sum of
all individuals that will be infected during the whole progress of the
epidemic.
在第一種情況下,最終死亡人數超過13,000人。此外,4月21日達到危重病人和每日死亡人數的峰值,如下圖所示,每天的死亡人數將達到每天155例的峰值。第二種情況導致約6,500人死亡,4月15日左右死亡人數達到高峰,每天約115人死亡。

The projected
development of the epidemic in Sweden, accounting for the actions taken around
March 12–16, assuming that the effects of the actions taken by the authorities
are less efficient than the ones taken in Hubei.

The number of
deaths in Sweden would peak around April 27, in case 1, and around April 15, in
case 2.
將繁殖數量降至0.88,而1.03,則產生了巨大的差異,在社會差異方面僅略有差異。這仍將在瑞典造成近6,500人死亡,然後疫情消失。
美國隔離
在我們的小調查中,假設從國外分發受感染病例,受感染者的數量及其流入美國是一個合適的參數。參數估計使用死亡數據完成,直到 3 月 31 日。美國的一個問題是,與瑞典和湖北相比,愛滋病在疫情發展方面存在較大的地區差異,不同州在不同時期採取了不同的行動。
下圖顯示了截至 3 月
31 日(圖表中的第 31 天)的模擬和報告死亡情況。此外,在這種情況下,我們看到死亡數呈指數級增長,對應於對數圖上的線性增長。

Simulated and
reported number of deaths in the U.S. as of March 31. Note that in the
logarithmic plot, the deviations between the model and the reported cases at
small values of deaths look larger than at larger numbers. The smaller graph
shows the same data in a logarithmic scale for the y-axis.
從美國數據參數估計中獲得的基本繁殖數為2.97,與瑞典(2.95)和湖北(3.03)的擬合值一致。進口個案總數約為8000宗。
同樣在美國,我們可以假設兩種情況:一種是減少社會互動的因素0.3,類似於瑞典的情況;另一種情況是降低互動水準,降低到上述湖北的情況,0.185。這也是合理的,因為美國在瑞典和湖北之間施加了限制;即,不是完全封鎖,而是比瑞典在社會交往方面受到更嚴格的限制。這給出的繁殖數量分別為0.89和0.55。
第一個場景預測,在疫情消失之前,有近2000萬美國人受到感染(見下圖)。截至4月1日,受感染人數為600萬。在第二種情況下,大約500萬人會感染。這大約是報告的確診病例的25倍,這再次聽起來像是高,但不太可能的數字,因為只有一小部分人口被測試。

Total number of
infected, accumulated, in the two case scenarios in the U.S. This is the sum of
all individuals that will be infected during the whole progress of the
epidemic.
在第一種情況下,美國的死亡人數將是11.5萬人(見下圖)。感染者的最大在3月24日左右。重症監護重症病例將於4月9日。在第二例中,與湖北一樣的限制,重症監護患者的數量將在4月1日左右達到高峰。在疫情消失之前,死亡人數約為33,000人。

Exposed,
infectious, critical, and deaths for the two case scenarios, one with a
reduction of reproduction number down to 0.89 (case 1), and a second with a
reduction down to 0.55 (case 2).

The number of
deaths in the U.S. would peak around April 15, in case 1, and around April 9,
in case 2, according to our model.
每天的死亡人數將在4月15日左右達到頂峰,如果是1,在4月9日左右,2。這相當於這兩例病例每天的死亡人數略低於1900人或1300人。我們可以看到,病例1給一個更大的時期,每天的死亡人數更多。而且數位很快就會變得更糟。如果我們將繁殖數量減少到1.04(再降低0.35倍)——即僅高於上述第1例——那麼,我們將在疫情結束之前觀察35萬例死亡。該模型清楚地顯示了社會疏遠的巨大影響,不僅在每天處於疫情危急狀態的人數,而且在疫情消失之前,受感染者總數也少得多。
發生新爆發時會發生什麼情況?
實施嚴格限制,迅速消滅流行病的問題是,人口仍然極易感染這種病毒。如果出現新的感染病例,那麼只有一小部分人可以免疫,在第二次疫情中,該流行病將再次以指數級增長的方式發展。這意味著,這樣一個社會必須準備非常迅速地採取行動對付新的疫情。實施較少的限制使第一次疫情的死亡人數增加,但它使更多的人群免疫,使這種人群在下一次疫情中變得不那麼脆弱。如果實施這種戰略,必須保護人口中有較高死亡率的部門,例如老年人。在第二次疫情中,這些人將受到免疫個體緩衝的保護。
如何使用模型
此處顯示的結果不應解釋為預測。它們是來自簡化現實的模型的結果。我們沒有考慮到人口統計學。例如,人口年齡分佈對疾病死亡率有很大影響。
在所研究的國家中,該流行病的進展處於不同階段,其地理差異也沒有準確解釋。人們如何往返於一個國家不同地區之間,也影響到這一流行病的進展。
此外,我們很難預測中國、瑞典和美國人民對模型的投入所採取的行動的影響。中國疾病預防控制中心、瑞典公共衛生局和美國疾病控制中心(CDC)等政府機構擁有更複雜的模型,包括年齡分佈、流行地點、城市間交通數據、進出國運數據以及其他人口統計數據。他們也有關於病毒和疾病本身的更好的數據,如不同條件和年齡分佈的潛伏時間和繁殖數量。
然而,使用此處介紹的模型仍然很有趣。他們瞭解這一流行病的動態。這些模型還有助於瞭解透過保持社會距離和避免不必要的社會互動來減少COVID-19的繁殖數量的重要性,減少受感染病人在重症監護中的峰值,並減少該流行病的總體影響。此外,Erlang_SEIR模型是參與公共衛生的國家和國際機構為城市和國家開發的更複雜的模型的重要組成部分和組成部分。
翻譯COMSOL 部落格文章,原始出處:
https://www.comsol.com/blogs/modeling-the-spread-of-covid-19-with-comsol-multiphysics/